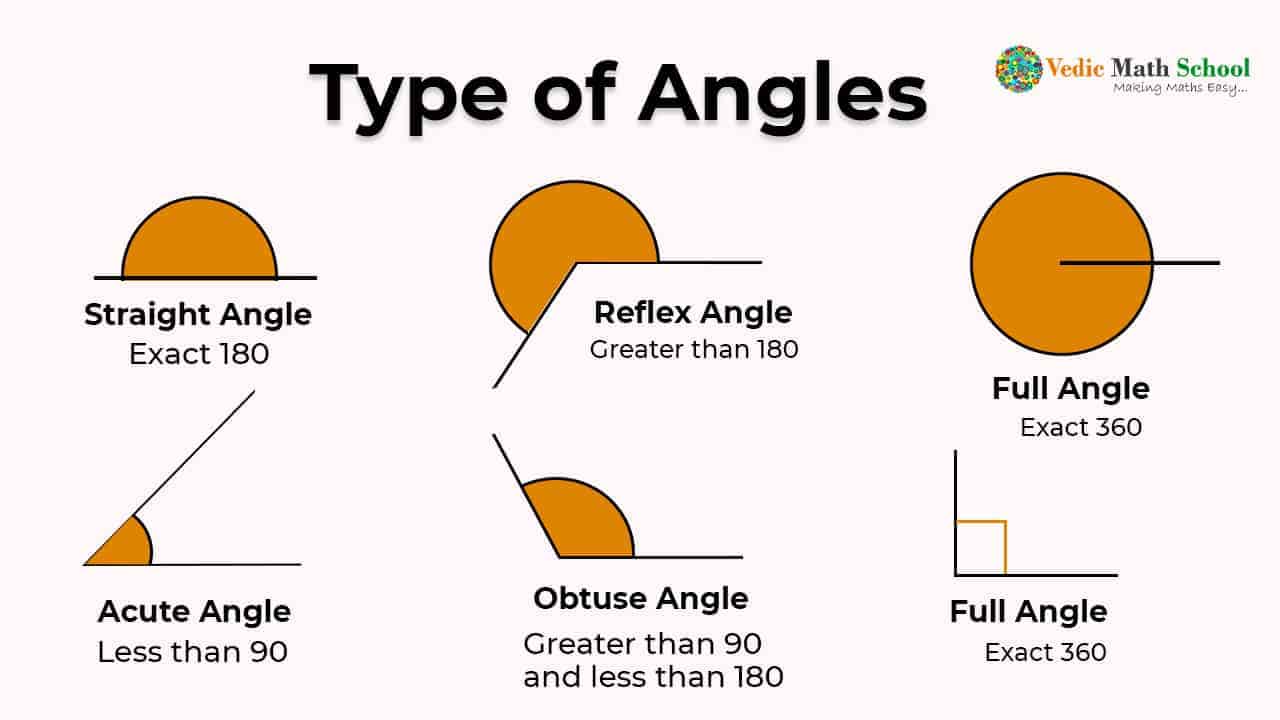
Have you ever found yourself looking at a number like 90 degrees and then, moments later, seeing something like pi over two, wondering if they were somehow related? It's a common thought, really. Angles, you see, are a fundamental part of how we describe turns, slopes, and positions in the world around us. From the way a car turns a corner to the path a satellite takes around our planet, angles are there, playing a quiet yet very important part. So, it's almost like they're the secret language of movement and shape.
There are, in fact, different ways to talk about these turns and slopes. Most of us grow up quite familiar with "degrees," where a full circle is a neat 360 units. It feels very intuitive, doesn't it? You can picture a quarter turn as 90 degrees, or half a turn as 180 degrees, just like that. But then, there's this other way, called "radians," which might seem a little less obvious at first glance. Yet, in many areas of serious thinking and figuring things out, radians are, as a matter of fact, the preferred way to go.
This is precisely where an angle degree to radian converter comes into its own. It's a simple tool, really, but one that bridges these two ways of expressing angles, making it much easier to switch between them as needed. Whether you're working on a school project, building something, or just trying to get a better handle on how angles work in different situations, knowing how to change degrees into radians, and vice versa, can be quite a useful skill. We'll talk about what this means for you, and why this simple conversion is actually pretty helpful.
- Nikola Jokic Family
- How Many Grammys Does Christina Aguilera Have
- Kate Spade Bag Blue
- Ryan Grantham Age
- Noah Ohlsen Age
Table of Contents
- What's the Big Deal About Angles, Anyway?
- Why Would Anyone Need an Angle Degree to Radian Converter?
- How Does an Angle Degree to Radian Converter Actually Work?
- What Makes Radians So Special for an Angle Degree to Radian Converter?
- A Little History of Measuring Angles for Your Angle Degree to Radian Converter
- Avoiding Common Slip-Ups with Your Angle Degree to Radian Converter
- Who Really Benefits from an Angle Degree to Radian Converter?
- The Future of Angle Measurement and the Angle Degree to Radian Converter
What's the Big Deal About Angles, Anyway?
Angles are a pretty basic idea, yet they show up in so many places. Think about it: a door swings open, a car turns a corner, or a robot arm picks something up. All of these movements involve angles. We use angles to describe how much something has rotated, how steep a slope is, or the spread between two lines. It’s like a universal language for describing orientation and rotation, you know? Without a way to measure these things, a lot of what we do in building, designing, and even just moving around would be much harder.
From the way a carpenter cuts a piece of wood to the path a satellite takes around our planet, angles are absolutely everywhere. They help us make things fit together, predict where something will go, and even understand the patterns in nature. So, in a way, knowing about angles helps us make sense of the physical world. It’s a very practical kind of knowledge, actually, and something we use more often than we might realize in our daily comings and goings.
Degrees and Radians - Two Ways to Look at an Angle Degree to Radian Converter
When it comes to talking about angles, there are two main systems people use. The one we're probably most familiar with is degrees. In this system, a full circle is split into 360 equal parts. So, if you turn all the way around, you've turned 360 degrees. A half turn is 180 degrees, and a quarter turn is 90 degrees. This system is pretty old, going back to ancient times, and it's easy to picture, which is why it's still so popular for everyday uses, or, like, for directions and stuff.
- Carrie Underwood Costume Ideas
- Hailee Steinfeld
- Daddy Yankee Nickname
- Tucker Carlson Response
- Immediate Wedding Los Angeles
Then there are radians. This system is a bit different because it connects the angle directly to the radius of a circle. Imagine a circle, and you draw a line from the center to the edge (that's the radius). Now, if you measure a piece of the circle's edge that is exactly the same length as that radius, the angle formed at the center by those two lines is one radian. A full circle, in radians, is about 6.28 units, or more precisely, two times pi. This might sound a little less straightforward at first, but for things like higher-level math and physics, radians are actually much more natural to work with. That's where an angle degree to radian converter really comes in handy.
Why Would Anyone Need an Angle Degree to Radian Converter?
You might be thinking, "If degrees are so easy, why bother with radians at all, and why would I need an angle degree to radian converter?" Well, it turns out that different fields of study and different kinds of work tend to use one system over the other. For example, in building and surveying, degrees are very common. It’s simple to measure with a protractor, and everyone understands what a 45-degree angle looks like. So, for a lot of practical, hands-on tasks, degrees are the go-to choice.
However, when you move into areas like advanced physics, engineering, computer graphics, or even music theory, radians often become the standard. The formulas used in these fields often work out much more neatly when angles are expressed in radians. It’s a bit like how some countries use miles and others use kilometers; you need a way to switch between them to make sure everyone is on the same page. That's why an angle degree to radian converter is pretty useful, especially if you're dealing with different kinds of information or working with people who prefer one system over the other.
Everyday Uses for an Angle Degree to Radian Converter
So, where might you actually run into a need for an angle degree to radian converter? Think about someone programming a video game. When a character jumps or a camera spins, the code behind it often uses radians for its calculations because the mathematical functions in programming languages are usually set up that way. Or consider an engineer designing a robotic arm; the motors and sensors might communicate their positions in degrees, but the equations to figure out how the arm moves through space might require radians. In these cases, a converter helps bridge that gap, making sure everything works together smoothly. It's a very practical bridge, in a way.
Even in fields like astronomy, when tracking the path of planets or satellites, angles are often measured in radians for more precise calculations. If you're a student learning about waves or oscillations in physics, you'll find that the equations for these phenomena are much simpler and more elegant when using radians. Basically, if you're ever dealing with a situation where you need to connect real-world measurements (often in degrees) with mathematical models or computer programs (often using radians), an angle degree to radian converter becomes a pretty handy tool to have around, like your own little translator for numbers, you know?
How Does an Angle Degree to Radian Converter Actually Work?
The core idea behind changing degrees to radians, or the other way around, is actually pretty straightforward. It all comes back to that full circle. We know a full circle is 360 degrees. We also know that a full circle is two times pi radians. So, if you have these two facts, you can set up a simple relationship. It's like saying that 360 degrees is exactly the same amount of turn as two pi radians. This connection is the key to how any angle degree to radian converter does its job, really.
Because 360 degrees and two pi radians represent the same complete turn, we can create a conversion factor. If you want to go from degrees to radians, you multiply your degree value by the ratio of (two pi radians) divided by (360 degrees). If you want to go from radians to degrees, you multiply your radian value by the ratio of (360 degrees) divided by (two pi radians). It’s a simple proportion, honestly, and once you grasp that, the converter just does the number crunching for you. It’s just a matter of applying that consistent relationship, which is, you know, pretty cool.
The Simple Math Behind the Angle Degree to Radian Converter
Let's break down the basic math that powers an angle degree to radian converter. To turn degrees into radians, you take your degree value and multiply it by the number pi, then divide that whole thing by 180. So, if you have 90 degrees, you'd calculate (90 * pi) / 180, which simplifies to pi over two radians. See? It’s not so bad, is that?
To go the other way, from radians to degrees, you take your radian value and multiply it by 180, then divide that by pi. So, if you have pi over two radians, you'd calculate (pi/2 * 180) / pi. The pi symbols would cancel each other out, leaving you with 180 divided by two, which is 90 degrees. This fundamental relationship is what every angle degree to radian converter uses behind the scenes. It's a consistent mathematical rule that makes switching between these two angle measurements a pretty simple task, more or less.
What Makes Radians So Special for an Angle Degree to Radian Converter?
You might still be wondering why radians are considered "special" or "natural" in some contexts, especially if degrees feel so much more straightforward. The main reason is that radians have a direct connection to the geometry of a circle in a way that degrees don't. When you're working with circles, arcs, and areas, using radians often simplifies the formulas you need to use. For example, the length of an arc on a circle is simply the radius multiplied by the angle in radians. If you used degrees, you'd have to include an extra conversion factor in your formula, which makes things a bit more cluttered, you know?
This direct relationship means that many mathematical concepts, particularly in calculus and trigonometry, become much more elegant and easier to work with when radians are used. It's like the math "prefers" radians because they strip away unnecessary conversion steps. This is why, for scientists, engineers, and mathematicians, an angle degree to radian converter is a useful tool for getting their numbers into the format that makes their calculations flow more smoothly. It’s just a more natural unit for certain kinds of mathematical expressions, basically.
Radians - A Natural Fit for the Angle Degree to Radian Converter
Consider the sine and cosine functions, which describe wave-like patterns. When you graph these functions using radians on the horizontal axis, their shapes are very clean and their properties are easy to see. If you used degrees, the graphs would look squished or stretched, and the relationships wouldn't be as obvious. This is because radians are tied to the actual length around a circle, which makes them inherently suitable for describing periodic phenomena, like waves, or even vibrations, and such. So, for anything that moves in a repeating pattern, radians tend to be the more appropriate measurement, and that's where an angle degree to radian converter helps bridge the gap from what we might measure in the real world.
Furthermore, in advanced mathematics, the derivatives and integrals of trigonometric functions are much simpler when angles are expressed in radians. This makes radians the preferred unit for higher-level scientific and engineering calculations. It's a subtle but powerful difference that makes a lot of complex math a little less complicated. So, when you see an angle degree to radian converter, think of it as a bridge to a more streamlined way of doing some pretty serious number work, which is pretty cool, actually.
A Little History of Measuring Angles for Your Angle Degree to Radian Converter
The idea of measuring angles isn't new at all; people have been doing it for thousands of years. The 360-degree system, for example, is thought to have come from the ancient Babylonians. They had a number system based on 60, and 360 is a multiple of 60 (6 x 60). Plus, 360 is a number that can be divided evenly by many other numbers (like 2, 3, 4, 5, 6, 8, 9, 10, 12, etc.), which made it very convenient for dividing circles for astronomical observations and practical building tasks. So, it made sense for them, in a way, to use that number.
Radians, on the other hand, are a much more recent invention, really. The concept started to take shape in the 1700s and became more formally defined in the 1800s as mathematics, especially calculus, developed further. As people began to explore more abstract and theoretical aspects of geometry and physics, the need for a unit that was more directly connected to the properties of a circle itself became clear. This shift shows how different tools and measurements come about as our ways of thinking and working evolve. So, the angle degree to radian converter is a pretty modern convenience, you know, compared to the old ways.
From Ancient Times to Your Angle Degree to Radian Converter
For a very long time, degrees were the only way most people measured angles. They were perfectly good for building pyramids, charting stars, and drawing maps. The simplicity of dividing a circle into 360 parts made it easy for everyone to grasp and use. It was, and still is, very practical for everyday applications where you need to visualize angles quickly, like when you're telling someone to turn 90 degrees to the left. That's a concept that is, you know, pretty easy to picture.
However, as mathematics became more abstract and began to describe things like wave motion, oscillations, and rotations in a more theoretical way, a different unit was needed. This is where radians stepped in. They offered a way to measure angles that was "dimensionless," meaning it wasn't tied to an arbitrary number like 360, but rather to a ratio of lengths (arc length to radius). This made them incredibly useful for theoretical work and complex calculations. So, the angle degree to radian converter is really a tool that helps us bridge these two historical paths of angle measurement, allowing us to use the best system for the job at hand, which is, frankly, pretty neat.
Avoiding Common Slip-Ups with Your Angle Degree to Radian Converter
Even with a simple tool like an angle degree to radian converter, it's possible to make a few little mistakes. One of the most common ones is simply forgetting which way you're converting. Are you going from degrees to radians, or radians to degrees? Mixing these up will, of course, give you the wrong answer. It's a bit like confusing kilometers with miles; the numbers will be off if you don't use the right conversion factor. So, it's always a good idea to double-check your starting unit and your desired ending unit before you punch in the numbers, or, you know, use the converter.
Another common slip-up involves the value of pi. Sometimes people might use a rounded version of pi, like 3.14, instead of the more precise value (which goes on forever). For most everyday uses, 3.14 might be fine, but for very precise scientific or engineering work, using a more accurate pi value is important. A good angle degree to radian converter will typically use a very precise value of pi, so you don't have to worry about that particular detail. It’s just something to keep in mind if you’re doing the math by hand, which, you know, some people still do.
Tips for Using an Angle Degree to Radian Converter Smoothly
To make sure you get the most out of an angle degree to radian converter, here are a few simple tips. First, always be clear about the unit of your input. Is it 45 degrees or 45 radians? This might sound obvious, but in a hurry, it's easy to overlook. Secondly, if you're using an online converter or a calculator, take a moment to understand how it works. Does it have separate buttons for degree-to-radian and radian-to-degree, or is there a single input field where you select the unit? Knowing this helps prevent errors, basically.
Also, it can be helpful to remember a few common conversions by heart. For instance, knowing that 180 degrees is pi radians, or that 90 degrees is pi over two radians, can give you a quick way to check if your converter's answer seems reasonable. If you convert 45 degrees and get something like 10 radians, you know something's probably off because 45 degrees is a quarter of 180 degrees, so it should be a quarter of pi. These little checks can save you time and help you feel more confident in your results. So, you know, just a little bit of practice can go a long way.
Who Really Benefits from an Angle Degree to Radian Converter?
It's fair to ask who actually uses an angle degree to radian converter in their daily lives or work. The truth is, quite a few different kinds of people find it pretty useful. Students, for one, especially those studying math, physics, or engineering, will absolutely encounter the need to switch between these units. It’s a standard part of their coursework and problem-solving. So, for them, a reliable converter is a study aid, in a way, that helps them grasp concepts and get their assignments done.
Beyond students, professionals in various technical fields rely on these conversions. Software developers working on computer graphics or animation often use radians for rotations in their code. Mechanical engineers designing gears, linkages, or robotic systems frequently need to convert between how parts are measured (often in degrees) and how their movements are calculated (often in radians). Even people in fields like surveying or navigation might use a converter if they're dealing with different mapping systems or instruments that use different angle units. It’s a tool that supports a lot of precision work, actually.
Different Folks, Different Needs for an Angle Degree to Radian Converter
Consider a physicist studying wave patterns. They'll almost certainly use radians because the equations describing waves are much simpler and more elegant when expressed in that unit. An architect, on the other hand, might draw blueprints using degrees because that's how their tools work and how contractors understand angles on a building site. But if that architect is using a computer program to simulate structural stress, that program might be doing its calculations internally using radians. So, the angle degree to radian converter becomes a bridge between the physical design and the digital analysis, you know?
Even in less obvious areas, like perhaps some specialized areas of music theory where angles are used to describe relationships between notes, or in certain types of art and design that involve precise geometric patterns, the ability to convert between degrees and radians can be quite helpful. It's about having the flexibility to work with the most appropriate unit for the specific task at hand, ensuring accuracy and making complex calculations a little bit easier to manage. So, it's a tool that helps a lot of different people, in a way, communicate across different numerical languages.
The Future of Angle Measurement and the Angle Degree to Radian Converter
As technology keeps moving forward, and as our understanding of the world gets more detailed, the need for precise and flexible measurement tools will only grow. The angle degree to radian converter, while a simple tool, represents this need for flexibility. In a world where different systems and standards coexist, the ability to seamlessly translate between them becomes more and more valuable. We might see converters becoming even more integrated into software, making the process almost invisible to the
- Yeezy Wiki
- Miami Dolphins Football Team
- Mgk Switch Genres
- Tolu Perfect Match
- Kevin Costner Cal Ripken