How To Convert From Degrees To Radians

Angles are a basic part of many things we work with, whether it's building something or figuring out how things move. You might know them best as degrees, which is a way we measure how wide an angle opens. Yet, there is another way to talk about angles, one that comes up a lot in higher math and science. This other way is called radians, and it gives us a different way to think about the space a turn takes up. For anyone looking to get a firmer grasp on these ideas, figuring out how to move between these two systems becomes pretty useful.

So, you see, knowing about degrees is one thing, but getting to grips with radians opens up a few more doors, especially when you are looking at things like waves, circles, or anything that spins. It is, in a way, like having two different rulers for the same job; both measure, but they do it with different marks. When you need to put your thoughts into the language of math that computers or advanced tools use, radians are, well, usually the preferred choice, you know?

This little chat will help you make sense of these two angle systems and, more importantly, show you the simple steps to switch from one to the other. We will go over why this switch is something you might need to do and, then, really, how to convert from degrees to radians, so you can work with both with confidence. It is a skill that, as a matter of fact, comes in handy more often than you might think.

• Is Jeffrey Epstein Related To Theo Epstein
• Kathryn Frazer Net Worth
• Oldest Person With Mowat Wilson
• Sadhguru And Isha Foundation
• 21 Savage Gunna

Table of Contents

• What are Degrees, Anyway?
• A Quick Look at Degrees
• What are Radians, Then?
• Getting to Grips with Radians
• Why Do We Even Need to Know How to Convert from Degrees to Radians?
• When Do You Convert from Degrees to Radians?
• So, How Do You Convert from Degrees to Radians?
• A Step-by-Step Guide on How to Convert from Degrees to Radians
• What is the Formula for How to Convert from Degrees to Radians?
• Some Examples of How to Convert from Degrees to Radians
• Working Through How to Convert from Degrees to Radians
• Common Questions About How to Convert from Degrees to Radians
• What is the Relationship Between Degrees and Radians?
• A Few Things to Keep in Mind When You Convert from Degrees to Radians
• Tips for How to Convert from Degrees to Radians

What are Degrees, Anyway?

When we talk about angles, the idea of a "degree" is probably the first thing that comes to mind for many people. It is a way to measure how much an object has turned around a point. Think of a full circle, you know, a complete spin. We often say that a full circle has 360 of these units. This number, 360, is pretty old, going back to ancient times, and it is useful because it can be divided by many other numbers without leaving a remainder. So, splitting a circle into halves, quarters, or even thirds becomes quite simple with degrees. For instance, a half-turn is 180 of these units, and a quarter-turn is 90. This system, in a way, helps us describe turns and slopes in a way that is easy for most people to picture.

A Quick Look at Degrees

A degree, then, is a small piece of a circle's full turn. If you imagine cutting a pie into 360 equally sized slices, each slice would represent one degree. This makes it a pretty straightforward way to talk about angles in everyday life, from telling someone to turn 90 degrees at a corner to talking about the tilt of a roof. It is a system that, for instance, we use in many tools for building or even in sports. You might hear about a golfer's swing having a certain degree of rotation, or a carpenter needing to cut wood at a specific angle, usually given in degrees. It is a common way to measure, so, it is something we see quite often.

What are Radians, Then?

Now, let's talk about radians. This way of measuring angles might seem a little different at first, but it is actually very natural when you are thinking about circles. Imagine a circle. It has a center point and a distance from that center to its edge, which we call the radius. A radian is defined by how much you have to go around the edge of the circle, or its arc, so that the length of that arc is the same as the radius. It is a bit like wrapping the radius around the outside of the circle. When the length along the curve matches the length of the straight line from the middle to the edge, that angle at the center is one radian. It is a measure that, honestly, connects the angle directly to the circle's size.

• Machine Gun Kelly Genres
• Is Michael Houston Still Alive
• Rosie O Donnell Movies
• Brock Lesnar Highlights
• Boston Legal Imdb

Getting to Grips with Radians

So, if you take the radius of a circle and lay it along the curve of the circle's edge, the angle that this arc makes at the center is one radian. It turns out that you can fit about 6.28 of these radius lengths around the entire circle. More precisely, a full circle contains exactly two times pi (2π) radians. This means that 360 degrees is the same as 2π radians. This connection between the circle's radius and its circumference makes radians especially useful in math fields that work with things that spin or repeat, like waves or oscillations. It is, in some respects, a more "natural" unit for these kinds of problems, as it ties directly into the circle's own measurements. You will find that, for example, many formulas in physics and engineering simply look tidier when using radians.

Why Do We Even Need to Know How to Convert from Degrees to Radians?

You might be wondering why we even bother with radians if degrees seem to work just fine. The truth is, while degrees are easy to picture and use for many everyday tasks, radians offer a different kind of usefulness, especially in higher mathematics and various scientific fields. Many formulas that describe how things move in circles, how waves behave, or even how things oscillate, become much simpler and more elegant when angles are expressed in radians. For instance, if you are studying trigonometry beyond the basics, or if you are working with calculus, you will find that radians are the standard unit. It is, you know, a bit like how different countries use different units for length; sometimes you need to switch between them to make sense of things or to work with specific tools or systems. So, learning how to convert from degrees to radians is a way to speak the language of these more complex subjects.

When Do You Convert from Degrees to Radians?

You will often find yourself needing to convert from degrees to radians when you are using scientific calculators, computer programs, or specialized equations. For example, if you are programming a robot arm to move a certain amount, or designing a part that spins, the math behind it usually prefers radians. Physics classes, especially those dealing with rotational motion or wave mechanics, will almost always use radians. Also, when you get into calculus, the rates of change for trigonometric functions like sine and cosine are much simpler when the angles are in radians. It is, essentially, the common tongue for these kinds of calculations. If you are ever faced with an equation that includes 'pi' as part of an angle measurement, that is a pretty good sign you are working with radians and might need to know how to convert from degrees to radians for your input values.

So, How Do You Convert from Degrees to Radians?

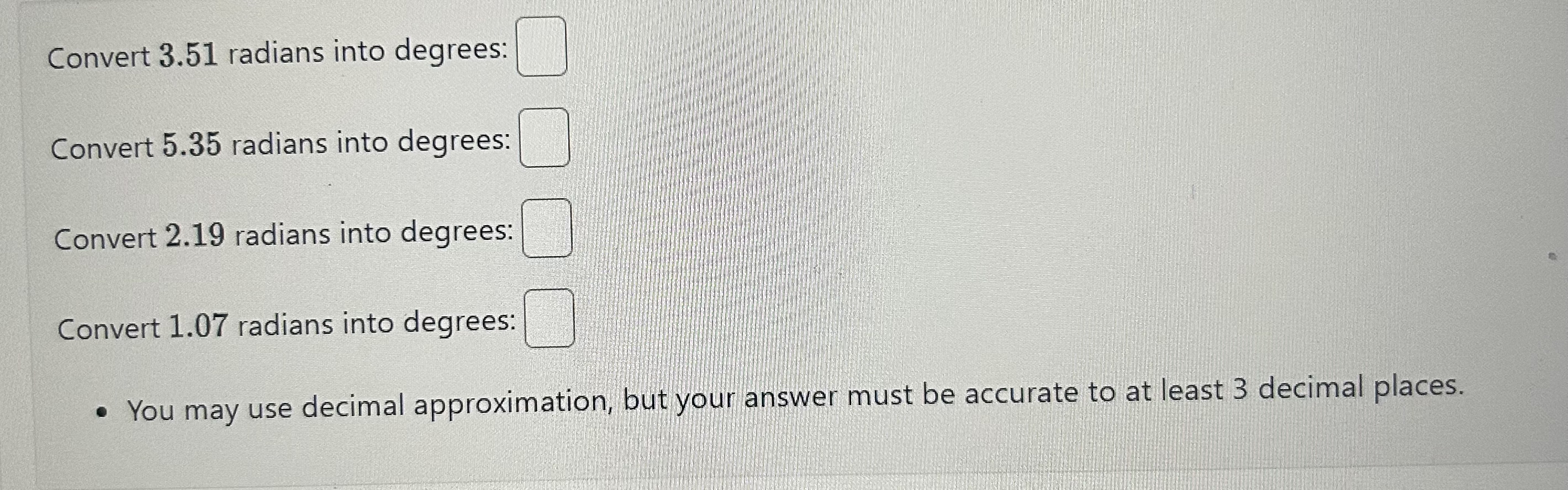
The good news is that converting from degrees to radians is actually quite straightforward. It all comes down to that one key relationship we talked about: a full circle, which is 360 degrees, is also 2π radians. This relationship gives us a direct way to set up a conversion factor. Think of it like converting between inches and centimeters; you have a fixed number that relates the two. For angles, that fixed number comes from the fact that 180 degrees is exactly the same as π radians. This fact is, you know, the backbone of the conversion process. Once you grasp this simple idea, the rest is just basic arithmetic. You can, for example, figure out any degree measurement in terms of radians by just multiplying it by the right fraction.

A Step-by-Step Guide on How to Convert from Degrees to Radians

To convert from degrees to radians, you just need to remember one simple fraction. Since 180 degrees equals π radians, you can create a ratio: (π radians) / (180 degrees). This ratio is your conversion factor. So, if you have an angle in degrees and you want to know what it is in radians, you just multiply your degree value by this fraction. The "degrees" unit in the bottom of the fraction will cancel out the "degrees" unit of your angle, leaving you with radians. It is, you know, a neat little trick to make sure your units work out correctly. This method makes figuring out how to convert from degrees to radians a very simple task, really, for any angle you might encounter.

What is the Formula for How to Convert from Degrees to Radians?

The formula for how to convert from degrees to radians is this:
Radians = Degrees × (π / 180)

Let's break this down a little bit. 'Degrees' here is the number of degrees you start with. 'π' (pi) is that special number, roughly 3.14159. The '180' is, well, 180, which comes from the fact that 180 degrees makes half a circle, and half a circle is also π radians. So, you are essentially finding out how many '180-degree chunks' are in your angle and then multiplying that by 'π' to get the radian equivalent. This formula is, honestly, the heart of knowing how to convert from degrees to radians. It gives you a straightforward path to getting the answer you need.

Some Examples of How to Convert from Degrees to Radians

Let's try a few examples to see how this works in practice. Suppose you have an angle of 90 degrees. You want to know what that is in radians. Using our formula, you would take 90 and multiply it by (π / 180). So, 90 * (π / 180). The 90 and the 180 can be simplified, giving you 1/2. So, 90 degrees is π/2 radians. This is, you know, a common angle, so it is a good one to remember. Or, what if you have 45 degrees? You would do 45 * (π / 180). This simplifies to π/4 radians. These simple cases really help to show how to convert from degrees to radians in a clear way.

Working Through How to Convert from Degrees to Radians

Consider another angle, say 30 degrees. To find its radian equivalent, you would set up the calculation as: 30 × (π / 180). If you simplify the fraction 30/180, you get 1/6. So, 30 degrees is the same as π/6 radians. What about 270 degrees? This is three-quarters of a full circle. Using the formula: 270 × (π / 180). Both 270 and 180 can be divided by 90, giving you 3/2. So, 270 degrees becomes 3π/2 radians. These steps, you know, are pretty much the same for any degree measure. It is a consistent way to figure out how to convert from degrees to radians, making it a reliable method for all your angle conversion needs.

Common Questions About How to Convert from Degrees to Radians

People often have a few common questions when they start working with radians and degrees. One of the main ones is about why we use two different systems in the first place. As we talked about, degrees are great for general use and for visualizing angles, while radians are more natural for mathematical calculations involving circles, waves, and things that spin. Another question that comes up is whether π always has to be in the answer. For exact answers, yes, you will usually see π in the radian value. If you need a decimal answer, you would then put the numerical value of π into your calculation. This is, you know, something that just takes a little getting used to.

What is the Relationship Between Degrees and Radians?

The core relationship, as we have discussed, is that a full circle is 360 degrees, and it is also 2π radians. This means that half a circle is 180 degrees, and it is also π radians. This connection, 180 degrees = π radians, is the foundation for all conversions between the two. It is, in a way, the bridge that connects the two systems. If you remember this one fact, you can always work out the conversion factor. This relationship is, for example, what allows us to move seamlessly between what we see on a protractor and what we use in advanced math problems. It is a pretty fundamental idea when you are trying to figure out how to convert from degrees to radians.

A Few Things to Keep in Mind When You Convert from Degrees to Radians

When you are doing these conversions, there are a couple of things that are worth remembering. First, always make sure you are using the correct value for π. For most calculations, using 3.14159 or even just π on your calculator is perfectly fine. Second, remember that radians are often left in terms of π, especially in math problems, unless you are asked for a decimal answer. This means your answer might look like π/3 or 3π/4, rather than a long decimal number. This is, you know, a common way to express radian values because it is often more precise. So, keeping these points in mind will help you when you are figuring out how to convert from degrees to radians.

Tips for How to Convert from Degrees to Radians

To make the process of converting from degrees to radians even smoother, try to memorize a few common conversions. Knowing that 90 degrees is π/2 radians, 180 degrees is π radians, and 360 degrees is 2π radians can really speed things up. Also, practice is key. The more you work through examples, the more natural the conversion process will feel. You can even try drawing circles and marking angles in both degrees and radians to get a better visual sense of how they relate. This can, you know, make the whole idea click into place more easily. So, with a little practice, figuring out how to convert from degrees to radians will become second nature.